隐马尔可夫模型和Viterbi算法总结

一般方法遍历二叉树

隐马尔科夫模型（Hidden Markov Model）学习笔记，知乎上看到别人的一篇文章，精简一下，用自己的语言总结一下。

原文：如何用简单易懂的例子解释隐马尔可夫模型？ - 回答作者：Yang Eninala - 知乎。

关于Viterbi算法，直接总结Wikipedia上的例子。

示例背景

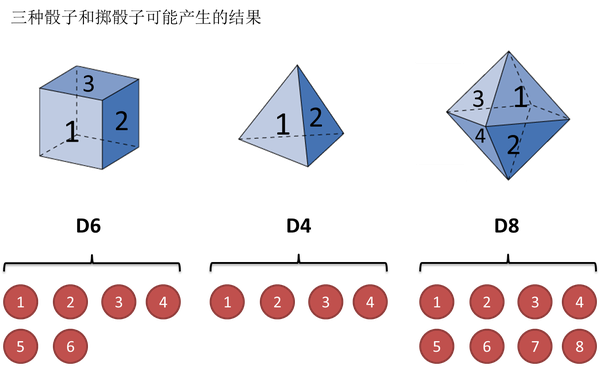
有三个骰子，分别是正四面体『D4』，正六面体『D6』，和正八面体『D8』，每个面都标有数字，正四面体标有1、2、3、4，每个面出现的概率为1/4，正六面体标有1、2、3、4、5、6，每个面出现的概率为1/6，正八面体标有1、2、3、4、5、6、7、8，每个面出现的概率为1/8。

隐马尔可夫模型

现在随机拿一个骰子，每个骰子被拿到的概率为1/3，然后扔骰子，会得到1-8数字中的某一个，一共扔了10次，得到一串数字1 6 3 5 2 7 3 5 2 4。

这串数字称为可见状态链。但在HMM中，我们不只有这一串可见状态链，还有一串隐含状态链。在本例中，隐含状态链就是扔的骰子的序列。比如，隐含状态链可能是：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8。

一般来说，HMM中的马尔科夫链指的是隐含状态链，因为隐含状态之间存在转换概率，本例中为了方便说明，状态之间的转换都是1/3，也就是说，当前骰子无论是D4、D6还是D8，下一个状态分别是D4、D6和D8的概率都是1/3。但实际上状态之间的转换可以有概率，如规定D6后面不能跟D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。

此外，尽管可见状态之间没有转换概率，但是隐含状态和可见状态之间有一个概率叫做输出概率。就本例而言，D6产生的各个面的概率都是1/6。同样我们也可以定义输出概率，如一个动过手脚的六面骰子，输出1的概率是1/2，输出其他数字的概率是1/10。

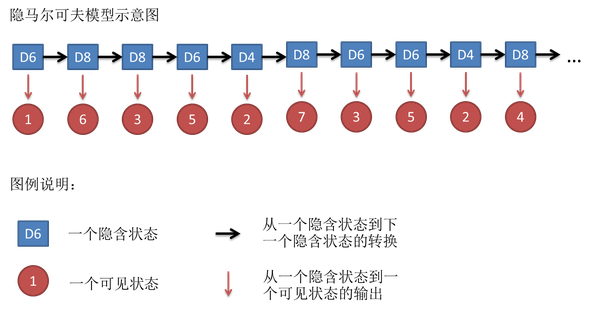
以上就一个隐马尔可夫模型的示例。

HMM相关算法

HMM相关算法主要分为三类。

已知骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道每次掷出来的都是哪种骰子（隐含状态链）。
还是知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道掷出这个结果的概率。
知道骰子有几种（隐含状态数量），不知道每种骰子是什么（转换概率），观测到很多次掷骰子的结果（可见状态链），我想反推出每种骰子是什么（转换概率）。

其中第三种情况，知道隐含状态数量，知道可见状态链，反推转换概率，是最常见的情况。

Viterbi算法

关于第三种情况，一种经典的算法叫做Viterbi算法。通过上面的学习，我们对HMM有了一个基本的了解，现在我们来看另一个例子。

假设某个村子里的所有村民不是『健康』就是『发烧』，并且只有村子里的医生可以判定村民是不是发烧了。医生通过询问村民的感觉判定村民是否发烧。村民只能回答感觉『普通』，『很冷』，或者『头晕』。

医生认为他的患者的健康状态是一个分离的马尔科夫链。该马尔科夫链中有两个状态，『健康』和『发热』，但是医生不能直接观察状态，状态被隐藏起来了。每天他的病人都会根据自己的健康状况告诉他，自己是觉得『普通』，『很冷』，或者『头晕』。

可见状态『普通，很冷，头晕』和隐藏状态『健康，发烧』组成了一个HMM，用Python语言表述如下：

states = ('Healthy', 'Fever')
observations = ('normal', 'cold', 'dizzy')
start_probability = {'Healthy': 0.6, 'Fever': 0.4}
transition_probability = {
    'Healthy' : {'Healthy': 0.7, 'Fever': 0.3},
    'Fever' : {'Healthy': 0.4, 'Fever': 0.6}
}
emission_probability = {
    'Healthy' : {'normal': 0.5, 'cold': 0.4, 'dizzy': 0.1},
    'Fever' : {'normal': 0.1, 'cold': 0.3, 'dizzy': 0.6}
}

上面这段代码中，start_probability表示当一个村民第一次来看病时医生认为的可能患病的概率『他只知道村民可能倾向于健康』。这里用的特定概率分布不是均衡的概率分布，并且是一个大概的概率{‘Healthy’: 0.57, ‘Fever’: 0.43}。transition_probability表示在马尔科夫链下的健康状态的转换。在本例子中，如果一个村民今天是健康的，那他明天发烧的概率只有0.3。emission_probability，表示村民今天可能的感觉。如果他是『健康』的，那他有0.5的概率觉得『普通』；如果他在『发烧』，则有0.6的概率觉得『头晕』。

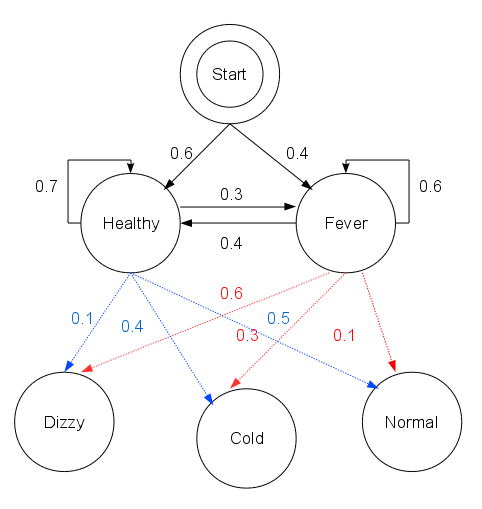
有一个患者，第一天说自己感觉『普通』，第二天感觉『很冷』，第三天感觉『头晕』，现在的问题是，医生怎么通过这个已知的状态序列，去判断这个患者的最可能的健康状态序列（上一小节中的第三种情况）。这里就需要用到Viterbi算法了。

Viterbi算法的动图如下所示。

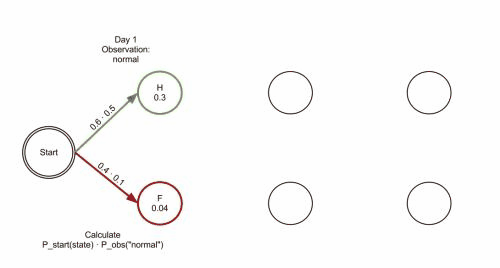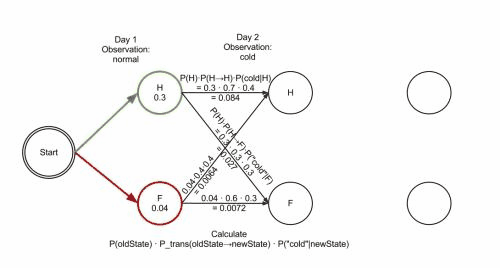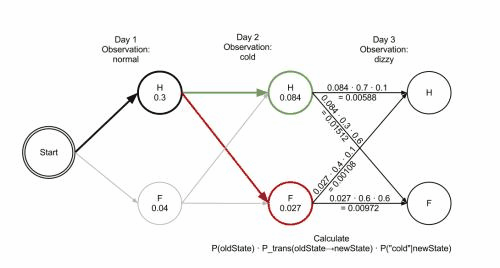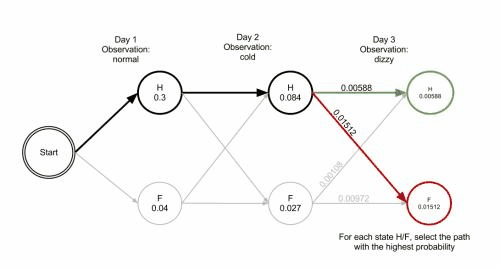
Viterbi算法的本质可以看做一种动态规划算法，下面我们通过逐步计算每天最可能的概率，来得出最可能的隐含状态序列（该患者最可能健康状态序列）。

Day 1

由于患者第一天来，医生认为患者『健康』的概率start_probability[‘Healthy’]=0.6，认为患者『发烧』的概率为start_probability[‘Fever’]=0.4。

又有已知输出状态：患者感觉『普通』。

则患者『健康』的概率为：
start_probability[‘Healthy’] × emission_probability[‘Healthy’][‘normal’] =
0.6 × 0.5 = 0.3
『发烧』的概率为：
start_probability[‘Fever’] × emission_probability[‘Fever’][‘normal’] =
0.4 × 0.1 = 0.04

即，
第一天健康的概率P[Day1_Healthy] = 0.3
发烧的概率P[Day1_Fever] = 0.04

由此得出第一天患者最可能的状态是『健康』。

Day 2

在求第二天的最可能隐含状态时，我们需要计算第一天所有转换状态下对第二天可见状态的影响。

已知输出状态：『很冷』。

假设第一天患者是『健康』的，第二天也是『健康』的（这里『健康』状态转『健康』状态的概率为0.7），则第二天『很冷』的概率为：
P[Day1_Healthy] × transition_probability[‘Healthy’][‘Healthy’] × emission_probability[‘Healthy’][‘cold’] =
0.3 × 0.7 × 0.4 = 0.084

假设第一天患者是『健康』的，第二天是『发烧』的（『健康』状态转『发烧』状态的概率为0.3），那则二天『很冷』的概率为：
P[Day1_Healthy] × transition_probability[‘Healthy’][‘Fever’] × emission_probability[‘Fever’][‘cold’] =
0.3 × 0.3 × 0.3 = 0.027

假设第一天患者是『发烧』的，第二天是『健康』的（『发烧』状态转『健康』状态的概率为0.4），那则二天『很冷』的概率为：
P[Day1_Fever] × transition_probability[‘Fever’][‘Healthy’] × emission_probability[‘Healthy’][‘cold’] =
0.04 × 0.4 × 0.4 = 0.0064

假设第一天患者是『发烧』的，第二天也是『发烧』的（『发烧』状态转『发烧』状态的概率为0.6），那则二天『很冷』的概率为：
P[Day1_Fever] × transition_probability[‘Fever’][‘Fever’] × emission_probability[‘Fever’][‘cold’] =
0.04 × 0.6 × 0.3 = 0.0072

由上可知，
第二天健康的概率P[Day2_Healthy] = 0.084
发烧的概率P[Day2_Fever] = 0.027

由此得出第二天患者最可能的状态是『健康』。

Day 3

已知输出状态：『头晕』

假设第二天患者是『健康』的，第三天也是『健康』的（『健康』状态转『健康』状态的概率为0.7），则第三天『头晕』的概率为：
P[Day2_Healthy] × transition_probability[‘Healthy’][‘Healthy’] × emission_probability[‘Healthy’][‘dizzy’] =
0.084 × 0.7 × 0.1 = 0.00588

假设第二天患者是『健康』的，第三天是『发烧』的（『健康』状态转『发烧』状态的概率为0.3），则第三天『头晕』的概率为：
P[Day2_Healthy] × transition_probability[‘Healthy’][‘Fever’] × emission_probability[‘Fever’][‘dizzy’] =
0.084 × 0.3 × 0.6 = 0.01512

假设第二天患者是『发烧』的，第三天是『健康』的（『发烧』状态转『健康』状态的概率为0.4），则第三天『头晕』的概率为：
P[Day2_Fever] × transition_probability[‘Fever’][‘Healthy’] × emission_probability[‘Healthy’][‘dizzy’] =
0.027 × 0.4 × 0.1 = 0.00108

假设第二天患者是『发烧』的，第三天也是『发烧』的（『发烧』状态转『发烧』状态的概率为0.6），则第三天『头晕』的概率为：
P[Day2_Fever] × transition_probability[‘Fever’][‘Fever’] × emission_probability[‘Fever’][‘dizzy’] =
0.027 × 0.6 × 0.6 = 0.00972

由上可知，
第三天健康的概率P[Day3_Healthy] = 0.00588
发烧的概率P[Day3_Fever] = 0.01512

由此得出第三天患者最可能的状态是『发烧』。

结论

通过上面的算法推倒，可得该患者最可能的健康状况序列为：『健康』，『健康』，『发烧』。上面的动图完整展示了Viterbi算法对本例的演算过程。

一般方法遍历二叉树

示例背景

隐马尔可夫模型

HMM相关算法

Viterbi算法

参考