概述
在统计学中,皮尔逊积矩相关系数(英语:Pearson product-moment correlation coefficient,又称作 PPMCC或PCCs, 文章中常用r或Pearson’s r表示)用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1之间。在自然科学领域中,该系数广泛用于度量两个变量之间的相关程度。它是由卡尔·皮尔逊从弗朗西斯·高尔顿在19世纪80年代提出的一个相似却又稍有不同的想法演变而来的。这个相关系数也称作『皮尔森相关系数r』
定义
两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商:

皮尔逊相关系数的变化范围为-1到1。系数的值为1意味着X和Y可以很好的由直线方程来描述,所有的数据点都很好的落在一条直线上,且Y随着X的增加而增加。系数的值为−1意味着所有的数据点都落在直线上,且Y随着X的增加而减少。系数的值为0意味着两个变量之间没有线性关系。
更一般的,我们发现,当且仅当Xi和Yi均落在他们各自的均值的同一侧,则(Xi−X)(Yi−Y)的值为正。 也就是说,如果Xi和Yi同时趋向于大于,或同时趋向于小于他们各自的均值,则相关系数为正。如果Xi 和Yi趋向于落在他们均值的相反一侧,则相关系数为负。
几何意义
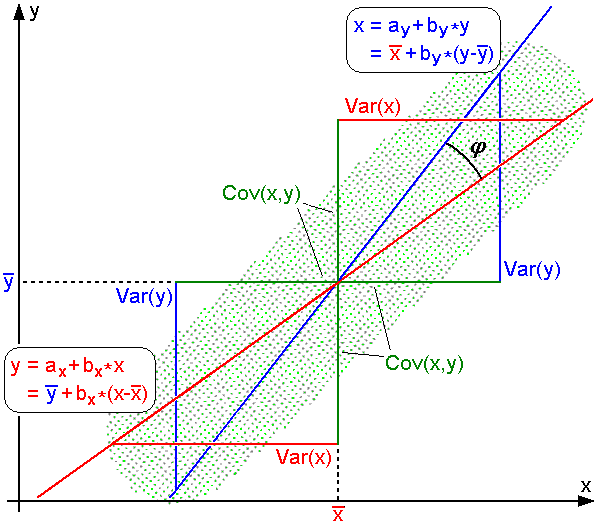
对于没有中心化的数据,相关系数与两条可能的回归线y=gx(x)和x=gy(y)夹角的余弦值一致。
对于中心化过的数据(也就是说,数据移动一个样本平均值以使其均值为0),相关系数也可以被视作由两个随机变量向量夹角的余弦值。
举例如下。
有5个国家的国民生产总值分别为10,20,30,50和80亿美元。假设这5个国家(顺序相同)的贫困百分比分别为11%,12%,13%,15%和18%。令x和y分别为包含上述5个数据的向量:x=(1,2,3,5,8)和y=(0.11,0.12,0.13,0.15,0.18)。
利用通常的方法计算两个向量之间的夹角(参见数量积),未中心化的相关系数是:
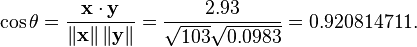
我们发现以上的数据特意选定为完全相关:y=0.10+0.01x。
于是,皮尔逊相关系数应该等于1。将数据中心化(通过E(x)=3.8移动x和通过E(y)=0.138移动y)得到x=(−2.8,−1.8,−0.8,1.2,4.2)和y=(−0.028,−0.018,−0.008,0.012,0.042),有:

总结地说,皮尔逊相关系数可以看做是两组向量中心化之后的夹角的余弦值。