机器学习笔记4：K近邻算法

K近邻算法简介

假定已有一些训练样本数据，且每个样本都存在数据标签，现在我们需要对一个新来的数据进行分类。显然我们能计算出该数据到样本集中所有数据的距离。

K近邻（K Nearest Neighbors）算法就是通过计算新数据到训练样本集中所有数据的距离，然后进行排序，取距离最小的K个样本中频度最高的分类。该分类就是新数据的分类。

示例

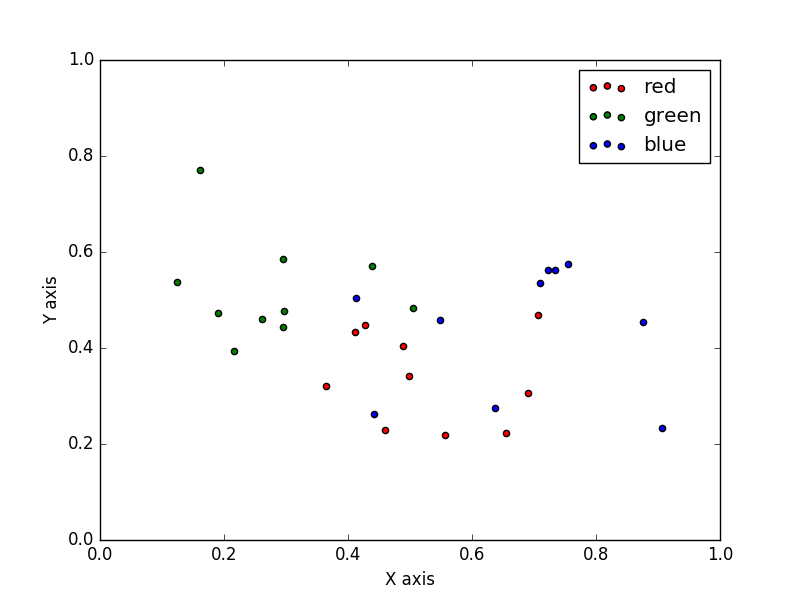
假定我们在二维空间有一些点，这些点被分为三类。如下图所示。

现在我们新加入一个点（下图黄点）。

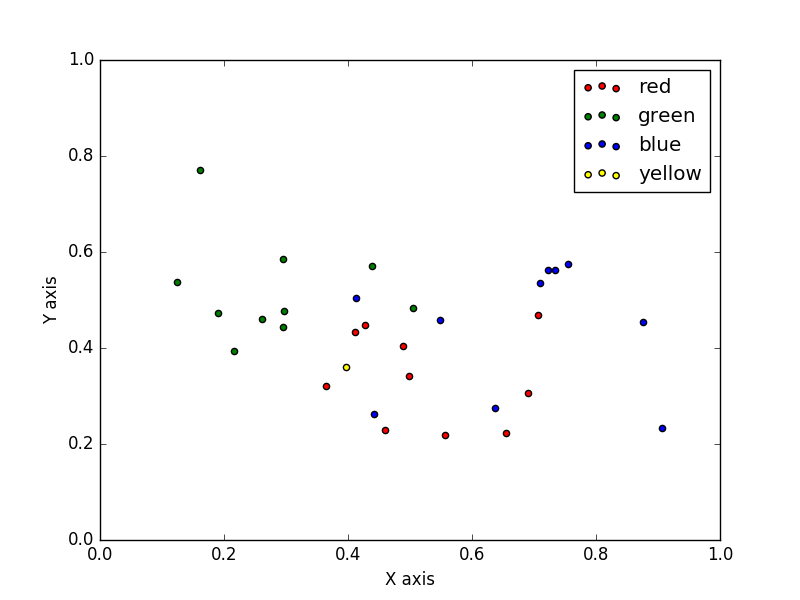
上图中黄点表示还未分类，显然我们可以通过计算得到该点到样本集中所有点的距离。

$$
\large
D = \sqrt {(x_a - x_b)^2 + (y_a - y_b)^2}
$$

求出的最近的N个距离最近的数据中，频度最大的分类即新数据的分类。

实际应用过程中，数据的维度一般不太可能只有两个维度，对于多维度空间，只需将求二维空间的距离转为求多维空间的欧氏距离即可，关于求欧氏距离的内容我们在前面的文章中已经讨论过。

Python实现

以下是Python代码的实现。

# -*- coding: utf-8 -*-
"""
K Nearest Neighbors
by Charles Ouyang
2016.06.20
"""
import math
import numpy as np
def cal_distance(vec1, vec2):
    """
    calculate the Euclidean distance of vec1 and vec2
    :param vec1:
    :param vec2:
    :return: distance
    """
    if len(vec1) != len(vec2):
        return -1
    return math.sqrt(sum(np.square(np.array(vec2) - np.array(vec1))))
def knn_classify(vec, data_set, labels, k):
    """
    K Nearest Neighbors algorithm
    :param vec: vector to be classified
    :param data_set: training data
    :param labels: labels of training data
    :param k: number of nearest neighbors to calculate
    :return: category of the vector
    """
    # store all the distances
    distances = []
    # store the sorted labels
    sorted_labels = []
    # iterate all vector in data_set
    for i, data in enumerate(data_set):
        # calculate the distance between current vector and vec
        cur_distance = cal_distance(vec, data)
        # insertion sort, insert current distance and label into the result lists(distance and sorted_labels)
        for j, stored_distance in enumerate(distances):
            if cur_distance < stored_distance:
                distances.insert(j, cur_distance)
                sorted_labels.insert(j, labels[i])
                break
        else:
            distances.append(cur_distance)
            sorted_labels.append(labels[i])
    # return the most common category in the list of top k sorted labels
    return most_common(sorted_labels[:k])
def most_common(lst):
    """
    get the most common element in a list
    http://stackoverflow.com/a/1518632/5772561
    :param lst:
    :return:
    """
    return max(set(lst), key=lst.count)
if __name__ == '__main__':
    # test code
    _data_set = [[1, 1, 2], [2, 2, 1], [3, 4, 6], [2, 7, 3], [2, 3, 4]]
    _labels = [1, 1, 2, 2, 2]
    _vec = [3, 8, 1]
    print(knn_classify(_vec, _data_set, _labels, 3))

KNN算法的优劣

优点：精度高、对数据不敏感、无数据输入假定。
缺点：计算复杂度高、空间复杂度高。
使用数据范围：数值型和标称型。

K近邻算法简介

示例

Python实现

KNN算法的优劣

参考