最小编辑距离

概述

最小编辑距离（Minimum Edit Distance）本身是的一个NLP中的一个概念，但实际上现代前端的MV?框架或者库中都有应用，值得学习一下。

编辑距离

两个字符串之间有多相似？

在搜索引擎中，我们总会有偶尔拼错单词的情况，但我们会发现，即便我们拼错了，搜索引擎也能正确地显示出我们想要的结果，而且还会温馨地给出拼写错误的提示。

如果我们在Google中检索”Gooogle”，我们会看到如下结果。

Showing results for google
Search instead for gooogle

Google知道我们输错了，但是它是怎么知道我们输错的呢？

同样地，在生物学中，我们想知道两段DNA或者RNA的有多相似，也会遇到类似的问题。

Seq1: AGGCTATCACCTGACCTCCAGGCCGATGCCC

Seq2: TAGCTATCACGACCGCGGTCGATTTGCCCGAC

对比结果：

Seq1: -AGGCTATCACCTGACCTCCAGGCCGA–TGCCC—

Seq2: TAG-CTATCAC–GACCGC–GGTCGATTTGCCCGAC

同样类似的场景还有很多，我们可以从中抽取出一个共通的问题，即从一个字符串转变为另一个字符串，需要经过怎样的编辑操作。

编辑距离和最小编辑距离

为了解决该问题，我们引入了编辑距离的概念，所谓的编辑距离，就是从串A转换到串B所需的编辑操作次数。

这里的编辑操作包括：

插入
删除
替换

而最小编辑距离（Minimum Edit Distance）就很容易理解了，就是从串A转换到串B所需的最少编辑操作次数（对应的代价）之和。

现在我们来考虑intention和execution两个单词之间的编辑距离。

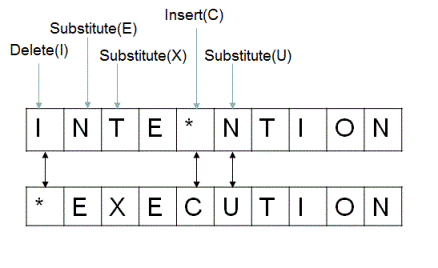
intention和execution之间的编辑距离

从上表可以看出，从intention到execution需要1次删除，3次替换，和1次插入。

如果我们把三种操作的代价都记为1，则其编辑距离为5。

除此之外还有一种计算方法将替换的记为2（即一次删除和一次插入），这种距离也被称为列文斯坦（Levenshtein）距离，此时的总距离为8。

动态规划求解MED

算法思想及伪码描述

求解MED最常用的方法采用了动态规规划的思想，计算过程中通过构建一张编辑距离表的方式，将串X到串Y的每一个编辑状态计算出来，每一步计算状态依赖于之前的计算状态。

# 伪码描述
D(i, 0) = i;
D(0, j) = j;
For each i = 1...M
	For each j = 1...N
		d1 = D(i - 1, j) + 1
		d2 = D(i, j - 1) + 1
		d3 = D(i - 1, j - 1) + X(i) === Y (j) ? 0 : 2
		D(i, j) = min(d1, d2, d3)

其中D(n, m)是距离，X(i)表示串X第i个位置的字符，Y(j)表示串Y第j个位置的字符。

编辑距离表

通过上述思想，我们可以构建一张编辑距离表。

首先初始化的时候其距离为，表的状态为：


N	9
O	8
I	7
T	6
N	5
E	4
T	3
N	2
I	1
#	0	1	2	3	4	5	6	7	8	9
	#	E	X	E	C	U	T	I	O	N

怎么理解这个表呢？

我们从倒数第二行开始，其第一列为#，表示一个空字符串，#到#对应的值为0，表示从一个空字符串到一个空字符串的MED为0。

#到E对应的值为1，表示从空字符串到E的MED为1，#到X对应的值为2，表示从空字符串到EX的MED为2，以此类推。

反过来，从第二列由下往上推也是同理。

现在我们完成了编辑距离表的初始化，接下来要完成整个表的填充。

实际上对于第D(n, m)的计算在伪码的描述中已经很明确了，就是求三个数值的最小值，第一个数值是表中当前位置的左边的数值 + 1，第二个数值是当前位置下面的数值 + 1，第三个数值相对复杂一点，如果当前位置对应的两个字符一样，则第三个数值就是左下角的数值，表示不需要做任何编辑，否则的话左下角的数字 + 2，表示是一次替换操作（这里认为一次替换操作的代价是2）。

现在我们来求倒数第三行第三列的数值，从上表可以看出，d1 = 1 + 1，d2 = 1 + 1，d3 = 0 + 2，三个值的最小值为2，所以D(0, 0) = 2。


N	9
O	8
I	7
T	6
N	5
E	4
T	3
N	2
I	1	2
#	0	1	2	3	4	5	6	7	8	9
	#	E	X	E	C	U	T	I	O	N

同样的道理可以求出，D(1, 2) = min(2 + 1, 2 + 1, 1 + 2)，即3。

一直这样计算我们可以得出：


N	9
O	8
I	7
T	6
N	5
E	4
T	3
N	2
I	1	2	3	4	5	6	7	6
#	0	1	2	3	4	5	6	7	8	9
	#	E	X	E	C	U	T	I	O	N

接下来我们计算D(0, 6)，可以发现X(0)和Y(6)是相同的，都是'I'，所以这里的值应该是min(7 + 1, 7 + 1, 6 + 0)，即6。

一次类推，我们可以将整个编辑距离表计算出来。


N	9	8	9	10	11	12	11	10	9	8
O	8	7	8	9	10	11	10	9	8	9
I	7	6	7	8	9	10	9	8	9	10
T	6	5	6	7	8	9	8	9	10	11
N	5	4	5	6	7	8	9	10	11	10
E	4	3	4	5	6	7	8	9	10	9
T	3	4	5	6	7	8	7	8	9	8
N	2	3	4	5	6	7	8	7	8	7
I	1	2	3	4	5	6	7	6	7	8
#	0	1	2	3	4	5	6	7	8	9
	#	E	X	E	C	U	T	I	O	N

最终可以算出表中右上角的数值是8，也就是说从INTENTION到EXECUTION的最小编辑距离为8。

带追溯过程的最小编辑编辑

求得最小编辑距离的值是不够的，我们还可以将整个过程回溯的过程记录下来，即我们是怎么计算出8这个值的。


N	9↓	8↓	9←↙↓	10←↙↓	11←↙↓	12←↙↓	11↓	10↓	9↓	8↙
O	8↓	7↓	8←↙↓	9←↙↓	10←↙↓	11←↙↓	10↓	9↓	8↙	9←
I	7↓	6↓	7←↙↓	8←↙↓	9←↙↓	10←↙↓	9↓	8↙	9←	10←
T	6↓	5↓	6←↙↓	7←↙↓	8←↙↓	9←↙↓	8↙	9←	10←	11←↓
N	5↓	4↓	5←↙↓	6←↙↓	7←↙↓	8←↙↓	9←↙↓	10←↙↓	11←↙↓	10↙↓
E	4↓	3↙	4↙	5↙	6←	7←	8←↓	9←↙↓	10←↙↓	9↓
T	3↓	4←↙↓	5←↙↓	6←↙↓	7←↙↓	8←↙↓	7↙	8←↓	9←↙↓	8↓
N	2↓	3←↙↓	4←↙↓	5←↙↓	6←↙↓	7←↙↓	8←↙↓	7↙↓	8←↙↓	7↙
I	1↓	2←↙↓	3←↙↓	4←↙↓	5←↙↓	6←↙↓	7←↙↓	6↙	7←	8←
#	0	1←	2←	3←	4←	5←	6←	7←	8←	9←
	#	E	X	E	C	U	T	I	O	N

这样我们可以记录一整个编辑过程。

从上图的右上角开始，我们可以划出一条完整的追溯路径。

下表是从右向左填写的。


X	I	N	T	E	-	N	T	I	O	N
Y	-	E	X	E	C	U	T	I	O	N
Action	Delete	Substitute	Substitute		Insert	Substitute

是不是和本文一开始的那张图一模一样呢？

1次删除，3次替换，和1次插入，编辑距离正好是8。

JavaScript实现

以下是MED在JavaScript中的实现。

const calcMed = (str1, str2) => {
    const len1 = str1.length;
    const len2 = str2.length;
	const d = [];
    for (let i = 0; i <= len1; i++) {
        const r = [];
        for (let j = 0; j <= len2; j++) {
            if (0 === i) {
	            r.push(j);
            } else {
                if (0 === j) {
                    r.push(i);
                } else {
                    const d1 = d[i - 1][j] + 1;
                    const d2 = r[j - 1] + 1;
                    const d3 = d[i - 1][j - 1] + (str1[i - 1] === str2[j - 1] ? 0 : 2);
                    r.push(Math.min(d1, d2, d3));   
                }
            }
        }
       	d.push(r);
    }
    return d;
};

console.log(calcMed('intention', 'execution'));

Python实现

这里顺便也给出Python的实现。

def calcMed(str1 = '', str2 = ''):
  L1 = len(str1)
  L2 = len(str2)
  m = []
  for i in range(L1 + 1):
    r = []
    for j in range(L2 + 1):
      if i == 0:
        r.append(j)
      else:
        if j == 0:
          r.append(i)
        else:
          d1 = r[j - 1] + 1
          d2 = m[i - 1][j] + 1
          d3 = m[i - 1][j - 1] + (2 if str1[i - 1] != str2[j - 1] else 0)
          r.append(min(d1, d2, d3))
    m.append(r)
  return m


for r in calcMed('intention', 'execution'):
  print(r)

MED在前端方面的应用

我们开始的时候提到了，MED在现代前端的MV?框架中也有应用场景，实际上指的就是虚拟DOM的diff算法。

在DOM的列表diff过程中，无论是React还是Vue，都要求我们提供一个key属性，而且要求该key是唯一的，其实这个key就是diff时用来做新旧DOM列表对比的凭证（这也是为什么React/Vue要求我们为列表提供key的原因）。

不难看出，标准的MED算法的时间复杂度是O(n * m)，实际上在真正的DOM diff过程中，我们做了一定地假设和优化，使得算法的时间复杂度变成了O(n + m)，当然这样做的代价是我们不是每一次都能求得最优解，但从工程和生产的角度来说，这样的牺牲是值得的。

对此感兴趣的同学可以详细看一下参考2。

总结

本文简单介绍了一下MED的概念和标准的求解算法，并给出了JavaScript和Python的实现，最后介绍了一下MED在前端的一种经典应用场景，希望这些对读到这篇文章的同学有一定帮助。

最小编辑距离还有一种加权最小编辑距离的形式，用于处理某些改动频率不一的情况，本文不再赘述，感兴趣的同学可以查看参考1。