Riact开发笔记之Diff数据结构篇

概述

Riact框架中并没有什么场景需要用到特别复杂的数据结构，但是为了具体的实现，有些地方还是想写篇笔记提一下。

在上一篇文章中我们介绍基于最长上升子序列（Longest Increasing Subsequence）的Diff算法实现，但是其中却隐去了很多细节，那就是对于移动，删除，插入等操作到底应该用怎样的形式存储。

Riact更新DOM的过程

为了搞清楚我们应该怎样结合算法来选择合适的存储方式，首先需要知道Riact更新DOM的过程。

在调用setState方法时到底发生了什么一文中，我们介绍了React中为了优化DOM的更新而使用到的一种“事务”的设计，总结起来就是，处于事务中的操作都会把当前的需要更新的组件放到一个dirtyComponents的数组中，等到事务的结束阶段，在去进行批量更新视图的操作。

严格来说，这是React16之前的设计。

Riact中同样采用了这种设计，所以当我们在Diff的过程中发现了差异，我们并不急于立刻去真地更新DOM，同样地，我们会将操作（更新属性，替换，移动，删除，插入节点等）先存储起来，等到真正更新DOM的时候，再将存储起来的操作执行。

在React中，计算Diff的过程被称作Reconciliation，大多数中文文档将其翻译为“一致化”，“协调”，意思虽然是正确地，但对于刚开始接触这个概念的同学却难以理解，而reconcile本身有调节（矛盾）的意思，我们可以理解为新旧虚拟DOM是有矛盾（差异）的，这个过程就是使之一致（一致化）的过程。此外，真正更新DOM的过程被称作Commit阶段。

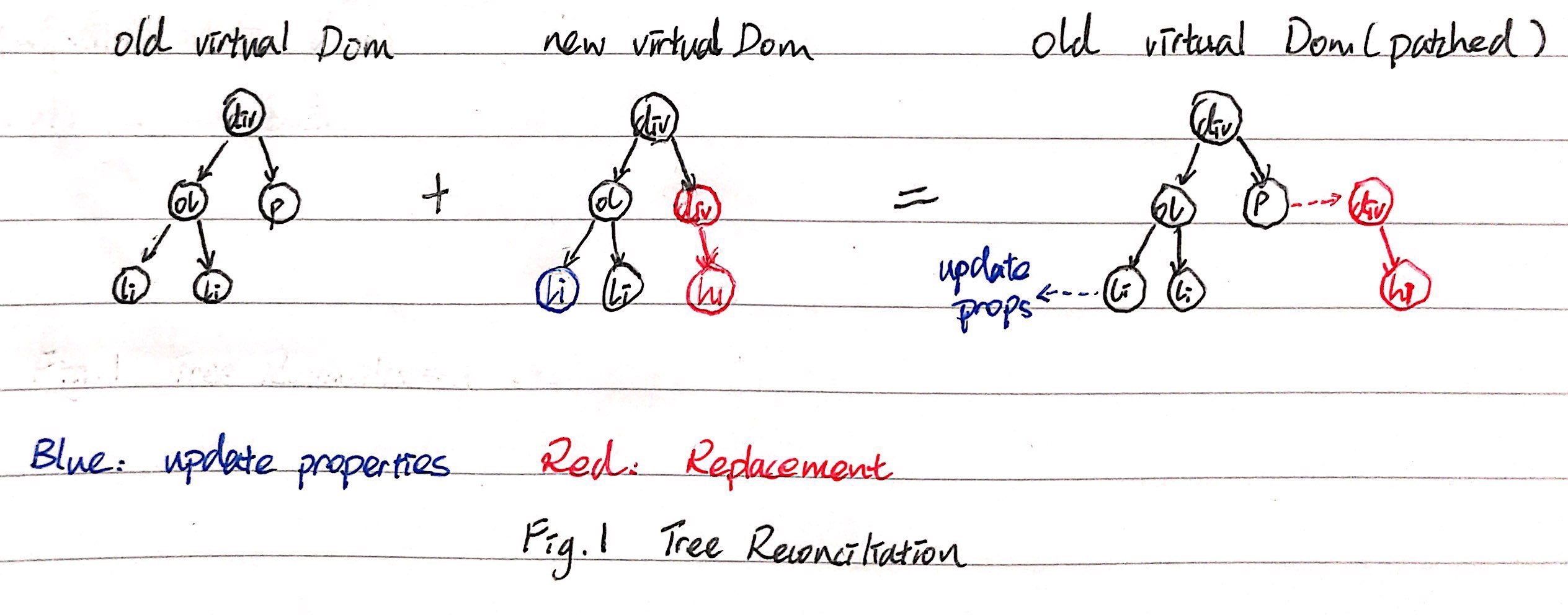
图1. Tree Reconciliation

从图1可以看出，当我们对两颗树进行对比之后，我们会将相关的操作都存储在旧的节点上，但此时我们不会直接更新它。

比如图1中有一个li节点需要被更新属性，这些新的属性都会被存在该节点的一个字段上（Riact中是patch字段），同样的，即便是替换，也会将新的DOM存起来，等到commit阶段（事务结束的时候）再拿出来。

列表更新

操作的存储

对于两棵树的协调和提交，基本上目前流行的前端框架都是只对同级节点进行对比，这里理解起来更简单，从上图中就能看出来。

关键的难点是列表的对比怎么处理，不难看出，在所有的操作中更新操作是容易处理的，只需要像上面一样，将待更新的操作存储到相同标记的旧节点上即可。

而对于删除、插入和移动操作，我们不能将其放到自身节点上。

首先对于插入操作，旧的列表中本来就没有对应的节点，将其存储到对应节点上也就无从说起；
对于移动操作，如果被移动的节点如果需要更新的情况下，我们就需要在该节点的patch属性上同时存储移动操作和更新操作，这样并不直观；
删除操作可以放到自身节点上，但为了便于处理，我们希望把删除和插入以及更新放到同一个层级上。

对于列表的这三种操作，它们其实并非是对单个节点的操作，而是对整个列表的操作，所以实际上Riact会将这些操作存储到列表的父节点上。

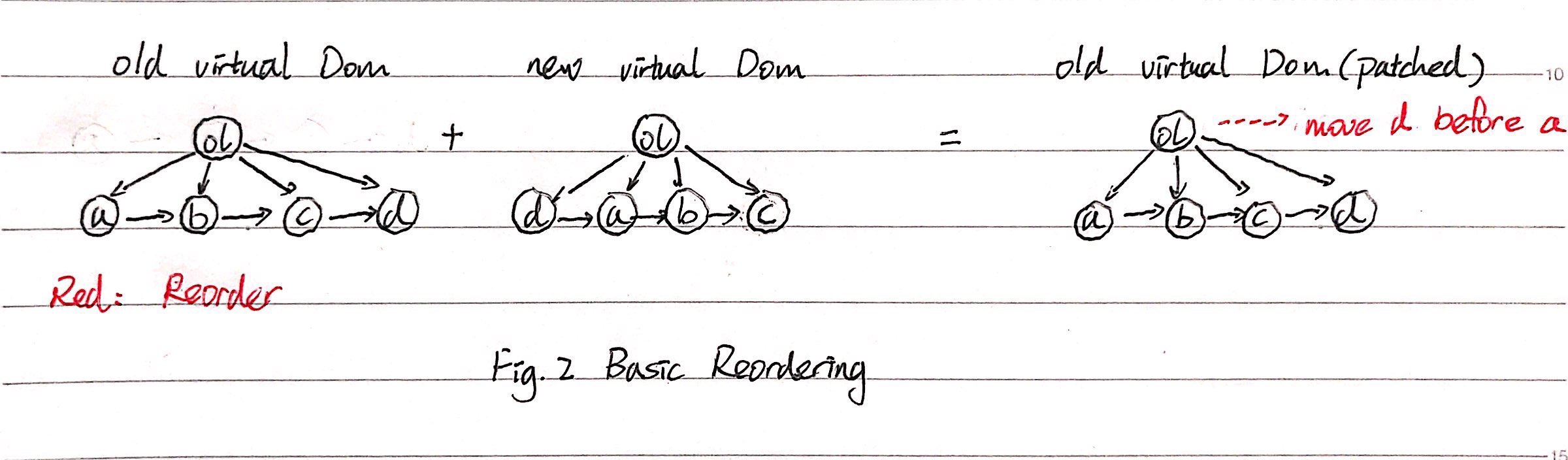
图2. Basic Reordering

事实上，列表节点的父节点中存储的操作分别会放到3个数组中，这3个数组分别存储了删除，移动和插入操作。

这里的列表都是带标记（key）的列表，Riact中对于在JSX中使用数组生成的节点并不支持不带key的情况。

顺序表的问题

到了一次事务结束的时候，我们开始更新真实的DOM，此时对于一个列表，增、删、移动的信息都已经能够拿到了。

在JavaScript中对一个数组的插入，删除，和移动，估计大多数同学对此都不会陌生，我们有很多很方便的方法能帮助我们达到目的，比如pop，push，shift，unshift，splice等等方法可以帮助我们操作数组，我们还有indexOf等方法可以帮助我们定位元素的位置。

但列表更新这个场景中这些方法真的可以被使用吗？在上一篇笔记的最后我写了一个小小的悬念：显然我们并不能用这些方法。

为什么呢？在JavaScript语言精粹一书中，Douglas提到shift和unshift的操作效率较低，实际上是从顺序表结构的存储来考虑的，由于一个数组在内存中是一串连续的地址，如果我们需要对数组的头部进行插入和删除，就意味着整个数组的后续元素都要被前移或者后移，仅仅是一次调用，其时间复杂度就已经达到了$\mathrm{O} \log n$，这是无法接受的，类似地，splice也是如此。

也许有的同学会说，既然这种方法效率如此之差，我们为什么还要使用它呢？其实如果不是对要求特别高，我们可以随意地使用它们，毕竟有这样的场景存在，而大多数实际场景下，顺序表的长度也不会特别大。但如果是开发底层基础设施的时候，这些方法会被频繁大量的调用，我们就不得不注意它们带来的影响了。

该用还是要用的，如果任何情况都纠结这些，那需求就做不完了。

链表的基本操作

需要对一个列表进行频繁的插入、删除和移动，我们很容易就想到链表（Linked List），这是数据结构中最基础的东西，这里就不再赘述了。

所以虚拟DOM的节点必须有一个nextSibling的属性，用来存储下一个兄弟节点。

需要注意的是，链表的插入，删除，需要获取的都不是真正要被操作的那个元素，而是该元素的前一个元素。

// 代码1. 链表的元素删除操作
// a --> b --> c --> d

// 如果需要删除c，我们需要存储的就是b节点
b.next = b.next.next

// 如果需要删除a，则直接将HEAD设置为b
HEAD.next = b

同样的插入也是一样。

// 代码2. 链表的元素插入操作
// a --> b --> c --> d

// 插入m到b后面
m.next = b.next
b.next = m

// 插入到链表的头部
m.next = HEAD.next
HEAD.next = m

对于移动某个节点，相当于是删除操作和插入操作的结合操作，所以不仅仅是被移动的节点的前继节点需要被存储，移动目标位置的前继节点也要存储。

// 代码3. 链表的元素移动操作
// a --> b --> c --> d

// 移动d到a后面
// 第一步，删除d并存储
N = c.next
c.next = c.next.next
// 第二步，将c插入到a后面
N.next = a.next
a.next = N

// 将d移动到表头
// 第一步，同上
// 第二步，将d插入到表头，参见代码2.

// 将a移动到表尾
// 第一步，删除a，参见代码1.
// 第二步，将a插入表尾，参见代码2.

可以看到为了操作链表，每一次操作需要存储的都是目标节点的前继节点，这就需要在我们实现Diff算法的时候去注意。

操作的实时更新

实现的过程还会遇到的一个问题是，在操作的进行过程中会打乱链表的顺序，考虑如下情况。

// 代码4. 被移动的链表操作
// a --> b --> c --> d
// 假设有如下操作
//   1. 删除b节点
//   2. 移动d节点到b节点的后面
// 如果按照顺序执行，在操作1删除b节点执行之后，操作2的执行将会失败，因为此时b节点已经被删除了

所以实际上三种操作都会打乱链表的顺序，所以在实施的过程中，Riact还需要维护一个对每个将被操作的节点前继节点的散列表来解决这个问题。

具体的代码可以参见Riact中的实现。

这一步的设计并不优雅，其实使用双向链表可能会好一些，但Riact的考虑的是尽量简化虚拟DOM节点的结构，所以并没有提供一个previousSibling这样一个属性，但双向链表显然也是能够实现同样的操作的。

总结

到这里为止，列表更新过程中需要注意到的数据结构方面的点已经基本被提到了，虽然还有一些细节，但这里没有办法做到面面俱到，如果对这方面感兴趣的同学，可以考虑自己去手动实现一个具备类似Reconciliation - Commit功能的虚拟DOM。

概述